GAMES101-L03 变换(二维与三维)
二维变换
线性变换
缩放
\[ \begin{bmatrix}x^{\prime} \\y^{\prime}\end{bmatrix}=\begin{bmatrix}s_x & 0 \\0 & s_y\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix} \]
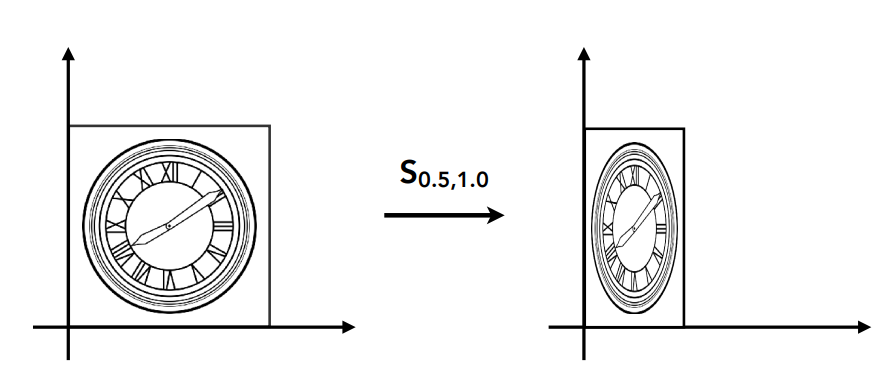
翻转
\[ \begin{bmatrix}x^{\prime} \\y^{\prime}\end{bmatrix}=\begin{bmatrix}1 & a \\0 & 1\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix} \]
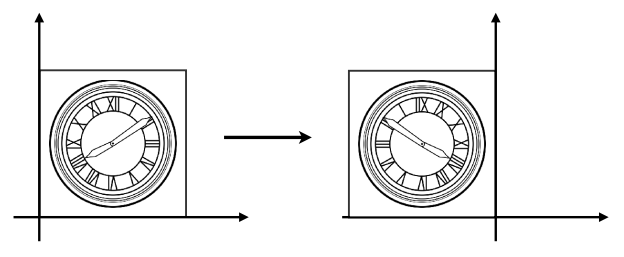
切变
\[ \begin{bmatrix}x^{\prime} \\y^{\prime}\end{bmatrix}=\begin{bmatrix}1 & a \\0 & 1\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix} \]
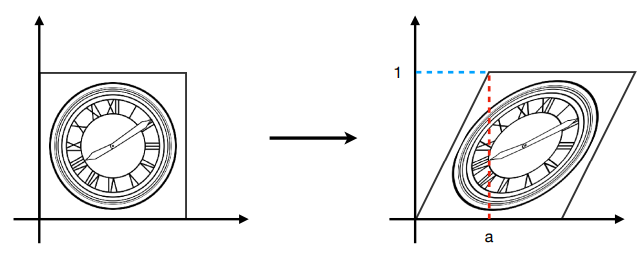
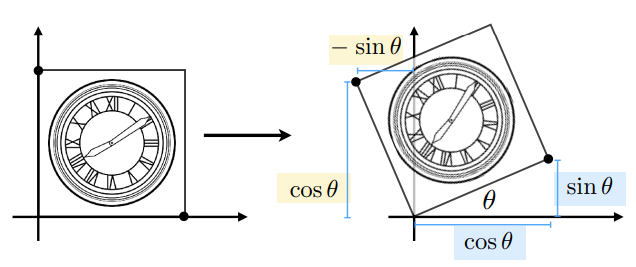
旋转
旋转时默认绕坐标原点旋转
\[ \mathbf{R}_\theta=\begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta\end{bmatrix} \]
旋转\(-\theta\) 时
\[ \mathbf{R}_{-\theta}=\begin{bmatrix}\cos \theta & \sin \theta \\-\sin \theta & \cos \theta\end{bmatrix}= \mathbf{R}_{\theta}^T= \mathbf{R}_{\theta}^{-1} \]
也就是旋转\(\theta\) 时的转置和逆运算
线性变换
\[ \begin{bmatrix}x^{\prime} \\y^{\prime}\end{bmatrix}=\begin{bmatrix}a & b \\c & d\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix} \]
平移
\[ \begin{bmatrix}x^{\prime} \\y^{\prime}\end{bmatrix}=\begin{bmatrix}a & b \\c & d\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix}+\begin{bmatrix}t_x \\t_y\end{bmatrix} \]
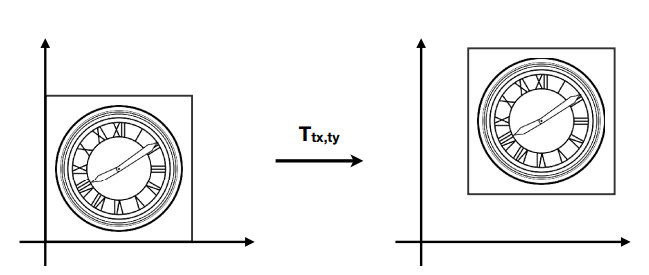
齐次坐标
点和向量的表示方法和计算
2D点 = \((x, y, 1)^{\top}\)
2D向量 = \((x, y, 0)^{\top}\)
向量+向量=向量
点-点=向量
点+向量=坐标
点+点=\(\begin{bmatrix}x / w \\y / w \\1\end{bmatrix}, w \neq 0\)
利用齐次坐标的进行平移变换
\[ \begin{bmatrix}x^{\prime} \\y^{\prime} \\w^{\prime}\end{bmatrix}=\begin{bmatrix}1 & 0 & t_x \\0 & 1 & t_y \\0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\1\end{bmatrix}=\begin{bmatrix}x+t_x \\y+t_y \\1\end{bmatrix} \]
二维仿射变换
仿射变换
仿射变换=线性变换+平移
\[ \begin{bmatrix}x^{\prime} \\y^{\prime} \\1\end{bmatrix}=\begin{bmatrix}a & b & t_x \\c & d & t_y \\0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\1\end{bmatrix} \]
缩放
\[ \mathbf{S}\left(s_x, s_y\right)=\begin{bmatrix}s_x & 0 & 0 \\0 & s_y & 0 \\0 & 0 & 1\end{bmatrix} \]
旋转
\[ \mathbf{R}(\alpha)=\begin{bmatrix}\cos \alpha & -\sin \alpha & 0 \\\sin \alpha & \cos \alpha & 0 \\0 & 0 & 1\end{bmatrix} \]
平移
\[ \mathbf{T}\left(t_x, t_y\right)=\begin{bmatrix}1 & 0 & t_x \\0 & 1 & t_y \\0 & 0 & 1\end{bmatrix} \]
逆变换
\(M^{-1}\) 在矩阵和几何意义上都是变换 \(M\) 的逆变换
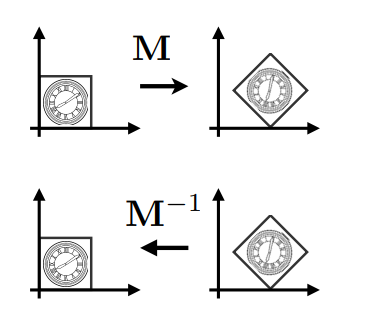
复合变换
完成以下变换:
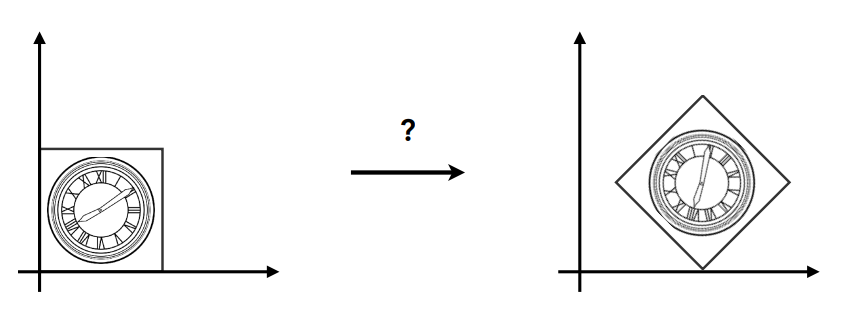
需要先旋转、再平移,因为旋转时以坐标原点为中心的:
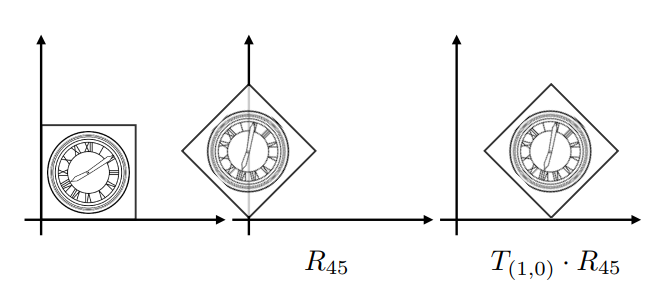
如果先平移、再旋转,则会得到已下结果:
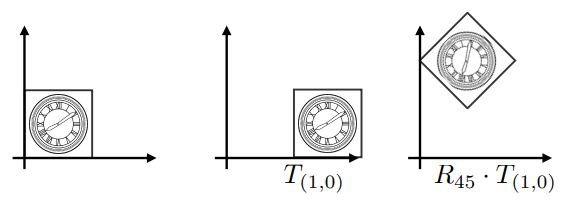
矩阵的乘法是没有交换律的,所以:
\(R_{45} \cdot T_{(1,0)} \neq T_{(1,0)} \cdot R_{45}\)
矩阵的计算是从右往左的:
\[ T_{(1,0)} \cdot R_{45}\begin{bmatrix}x \\y \\1\end{bmatrix}=\begin{bmatrix}1 & 0 & 1 \\0 & 1 & 0 \\0 & 0 & 1\end{bmatrix}\begin{bmatrix}\cos 45^{\circ} & -\sin 45^{\circ} & 0 \\\sin 45^{\circ} & \cos 45^{\circ} & 0 \\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x \\y \\1\end{bmatrix} \]
连续变换
如果有一个仿射变换序列A1,A2,A3,…
\[ \mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot\begin{bmatrix}x \\y \\1\end{bmatrix} \]
可以通过矩阵乘法的分配率来改变运算顺序,先算前面的 \(\mathbf{A}_n \cdots \mathbf{A}_2 \cdot \mathbf{A}_1 \cdot\),然后再和坐标向量相乘
分解复杂变换
如果需要旋转一个顶点不在坐标原点的图像,需要先将图像平移到坐标原点,再旋转,最后再平移回去
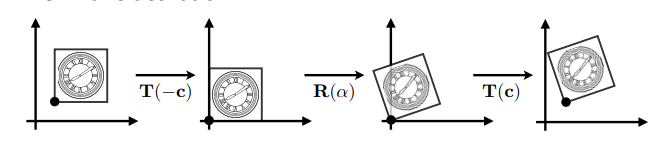
\(\mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c})\)
三维齐次坐标
3D点 = \((x, y, z, 1)^{\top}\)
3D向量 = \((x, y, z, 0)^{\top}\)
向量+向量=向量
点-点=向量
点+向量=坐标
点+点=\(\begin{bmatrix}x / w \\y / w \\z / w \\1\end{bmatrix}, w \neq 0\)
三维仿射变换
矩阵表示
\[ \begin{bmatrix}x^{\prime} \\y^{\prime} \\z^{\prime} \\1\end{bmatrix}=\begin{bmatrix}a & b & c & t_x \\d & e & f & t_y \\g & h & i & t_z \\0 & 0 & 0 & 1\end{bmatrix}\cdot\begin{bmatrix}x \\y \\z \\1\end{bmatrix} \]
仿射变换
缩放
\[ \mathbf{S}\left(s_x, s_y, s_z\right)=\begin{bmatrix}s_x & 0 & 0 & 0 \\0 & s_y & 0 & 0 \\0 & 0 & s_z & 0 \\0 & 0 & 0 & 1\end{bmatrix} \]
平移
\[ \mathbf{T}\left(t_x, t_y, t_z\right)=\begin{bmatrix}1 & 0 & 0 & t_x \\0 & 1 & 0 & t_y \\0 & 0 & 1 & t_z \\0 & 0 & 0 & 1\end{bmatrix} \]
旋转
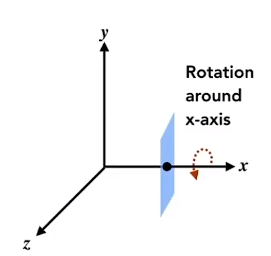
绕x轴旋转
x坐标不变
\[ \mathbf{R}_x(\alpha)=\begin{bmatrix}1 & 0 & 0 & 0 \\0 & \cos \alpha & -\sin \alpha & 0 \\0 & \sin \alpha & \cos \alpha & 0 \\0 & 0 & 0 & 1\end{bmatrix} \]
绕y轴旋转
y坐标不变
\[ \mathbf{R}_y(\alpha)=\begin{bmatrix}\cos \alpha & 0 & \sin \alpha & 0 \\0 & 1 & 0 & 0 \\-\sin \alpha & 0 & \cos \alpha & 0 \\0 & 0 & 0 & 1\end{bmatrix} \]
绕z轴旋转
z坐标不变
\[ \mathbf{R}_z(\alpha)=\begin{bmatrix}\cos \alpha & -\sin \alpha & 0 & 0 \\\sin \alpha & \cos \alpha & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{bmatrix} \]
罗德里格斯旋转公式
绕轴n旋转角度α,默认旋转轴n过原点
\[ \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^T+\sin (\alpha) \underbrace{\begin{bmatrix}0 & -n_z & n_y \\n_z & 0 & -n_x \\-n_y & n_x & 0\end{bmatrix}}_{\mathbf{N}} \]