GAMES101-L05 光栅化（三角形的离散化）

视锥

定义

宽度：\(width\)
高度：\(height\)

近平面：\(zNear\)
远平面：\(zFar\)
垂直可视角：长方形上下中点与相机连线的角度，\(fovY\)(Vertical Field of View)
宽高比：\(aspect\)

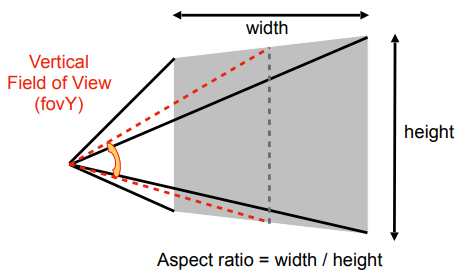
视锥体转换到视景体

需要计算出视景体的l,r,t,b,n,f信息
由于在此之前的视图变换，视景体n、f平面的中心就在Z轴上，而视锥体的近平面和远平面就是视景体的n,f。

视锥体参数和视景体存在以下关系：
\(\tan \frac{\text {fov } Y}{2}=\frac{t}{|n|}\)
\(\text{aspect}=\frac{r}{t}\)

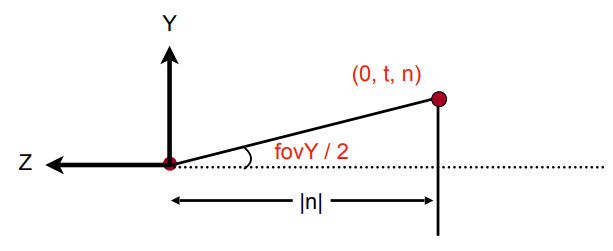
所以：
\(n=zNear\)
\(f=zFar\)
\(t=tan(\frac{fovY}{2} )\times n\)
\(b=-t\)
\(r=aspect\times t\)
\(l=-r\)

光栅化

屏幕

二维数组
数组大小：分辨率
典型的光栅显示器

光栅化：在屏幕上绘图

屏幕坐标系

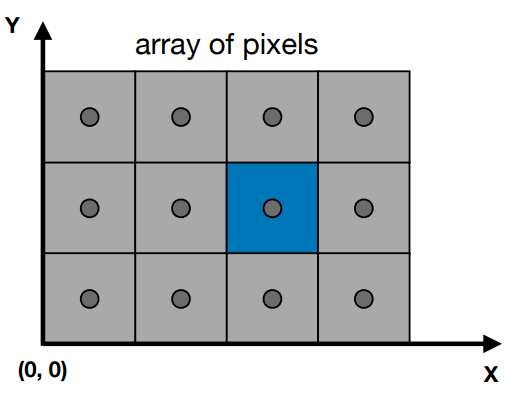
屏幕的左下角为原点
蓝色像素为 \((2,1)\)
用像素的左下角来表示像素，像素 \((x,y)\) 的中心在 \((x+0.5,y+0.5)\)
所有的像素坐标从 \((0,0)\) 到 \((width-1,height-1)\)
整个屏幕会覆盖 \((0,0)\) 到 \((width,height)\)

视口变换

将正交投影显示到屏幕

1.忽略z坐标
2.将\([-1,1]^2\)拉伸到\([0,width]\times[0,height]\)

\[ M_{\text {viewport }}=\begin{bmatrix} \frac{ width }{2} & 0 & 0 & \frac{ width }{2} \\ 0 & \frac{ height }{2} & 0 & \frac{ height }{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

光栅化

采样

采样就是获取每个点的函数值
采样是对函数的离散化

for (int x = 0; x < xmax; ++x)
    output[x] = f(x); 

光栅化就是2D的采样

光栅化

判断屏幕上的像素是否在三角形内部

\(\text { inside }(t, x, y) \begin{cases}1 & \text { Point }(x, y) \text { in triangle } t \\ 0 & \text { otherwise }\end{cases}\)

光栅化=对2D指示器函数进行采样

for (int x = 0; x < xmax; ++x)
   for (int y = 0; y < ymax; ++y)
       image[x][y] = inside(tri,
 x + 0.5, 
y + 0.5); 

inside函数：利用叉乘判断像素点的中心是否在三角形内部

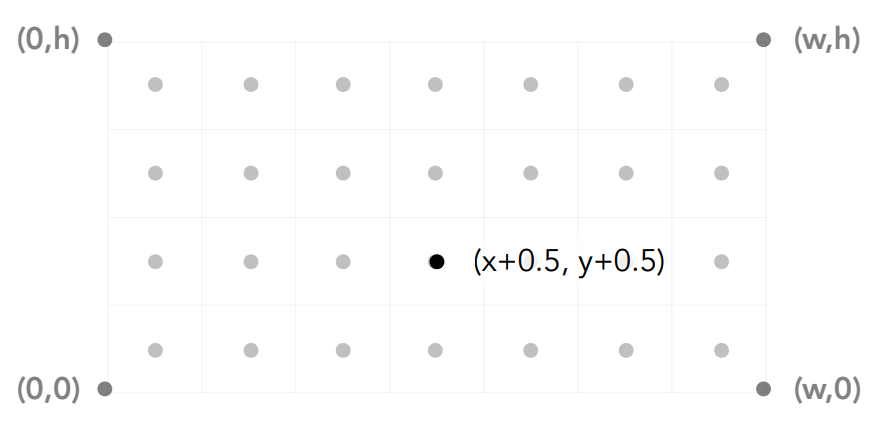
样本 (x,y) 的位置

优化

原本是判断屏幕上所有的像素是否在三角形内部，可以使用包围盒来只判断三角形周围的像素。