6.6 通过时间反向传播
定义模型
简单起见,考虑一个无偏差项的循环神经网络,且激活函数为恒等映射(\(\phi(x)=x\))。设时间步 \(t\) 的输入为单样本 \(\boldsymbol{x}_t \in \mathbb{R}^d\),标签为 \(y_t\),那么隐藏状态 \(\boldsymbol{h}_t \in \mathbb{R}^h\)的计算表达式为
\[ \boldsymbol{h}_t = \boldsymbol{W}_{hx} \boldsymbol{x}_t + \boldsymbol{W}_{hh} \boldsymbol{h}_{t-1}, \]
其中\(\boldsymbol{W}_{hx} \in \mathbb{R}^{h \times d}\)和\(\boldsymbol{W}_{hh} \in \mathbb{R}^{h \times h}\)是隐藏层权重参数。设输出层权重参数\(\boldsymbol{W}_{qh} \in \mathbb{R}^{q \times h}\),时间步\(t\)的输出层变量\(\boldsymbol{o}_t \in \mathbb{R}^q\)计算为
\[ \boldsymbol{o}_t = \boldsymbol{W}_{qh} \boldsymbol{h}_{t}. \]
设时间步\(t\)的损失为\(\ell(\boldsymbol{o}_t, y_t)\)。时间步数为\(T\)的损失函数\(L\)定义为
\[ L = \frac{1}{T} \sum_{t=1}^T \ell (\boldsymbol{o}_t, y_t). \]
将\(L\)称为有关给定时间步的数据样本的目标函数。
模型计算图
为了可视化循环神经网络中模型变量和参数在计算中的依赖关系,可以绘制模型计算图,如下图所示。
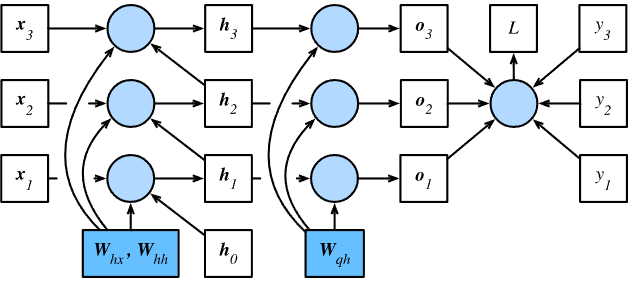
方法
刚刚提到,图中的模型的参数是 \(\boldsymbol{W}_{hx}\), \(\boldsymbol{W}_{hh}\) 和 \(\boldsymbol{W}_{qh}\)。训练模型通常需要模型参数的梯度\(\partial L/\partial \boldsymbol{W}_{hx}\)、\(\partial L/\partial \boldsymbol{W}_{hh}\)和\(\partial L/\partial \boldsymbol{W}_{qh}\)。 根据图6.3中的依赖关系,按照其中箭头所指的反方向依次计算并存储梯度。
首先,目标函数有关各时间步输出层变量的梯度\(\partial L/\partial \boldsymbol{o}_t \in \mathbb{R}^q\):
\[ \frac{\partial L}{\partial \boldsymbol{o}_t} = \frac{\partial \ell (\boldsymbol{o}_t, y_t)}{T \cdot \partial \boldsymbol{o}_t}. \]
下面,可以计算目标函数有关模型参数\(\boldsymbol{W}_{qh}\)的梯度\(\partial L/\partial \boldsymbol{W}_{qh} \in \mathbb{R}^{q \times h}\)。根据上图,\(L\)通过\(\boldsymbol{o}_1, \ldots, \boldsymbol{o}_T\)依赖\(\boldsymbol{W}_{qh}\)。依据链式法则,
\[ \frac{\partial L}{\partial \boldsymbol{W}_{qh}} = \sum_{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \boldsymbol{o}_t}, \frac{\partial \boldsymbol{o}_t}{\partial \boldsymbol{W}_{qh}}\right) = \sum_{t=1}^T \frac{\partial L}{\partial \boldsymbol{o}_t} \boldsymbol{h}_t^\top. \]
其次,注意到隐藏状态之间也存在依赖关系。 在上图中,\(L\)只通过\(\boldsymbol{o}_T\)依赖最终时间步\(T\)的隐藏状态\(\boldsymbol{h}_T\)。因此,先计算目标函数有关最终时间步隐藏状态的梯度\(\partial L/\partial \boldsymbol{h}_T \in \mathbb{R}^h\)。依据链式法则,得到
\[ \frac{\partial L}{\partial \boldsymbol{h}_T} = \text{prod}\left(\frac{\partial L}{\partial \boldsymbol{o}_T}, \frac{\partial \boldsymbol{o}_T}{\partial \boldsymbol{h}_T} \right) = \boldsymbol{W}_{qh}^\top \frac{\partial L}{\partial \boldsymbol{o}_T}. \]
接下来对于时间步\(t < T\), 在图中,\(L\)通过\(\boldsymbol{h}_{t+1}\)和\(\boldsymbol{o}_t\)依赖\(\boldsymbol{h}_t\)。依据链式法则, 目标函数有关时间步\(t < T\)的隐藏状态的梯度\(\partial L/\partial \boldsymbol{h}_t \in \mathbb{R}^h\)需要按照时间步从大到小依次计算:
\[ \frac{\partial L}{\partial \boldsymbol{h}_t} = \text{prod} (\frac{\partial L}{\partial \boldsymbol{h}_{t+1}}, \frac{\partial \boldsymbol{h}_{t+1}}{\partial \boldsymbol{h}_t}) + \text{prod} (\frac{\partial L}{\partial \boldsymbol{o}_t}, \frac{\partial \boldsymbol{o}_t}{\partial \boldsymbol{h}_t} ) = \boldsymbol{W}_{hh}^\top \frac{\partial L}{\partial \boldsymbol{h}_{t+1}} + \boldsymbol{W}_{qh}^\top \frac{\partial L}{\partial \boldsymbol{o}_t} \]
将上面的递归公式展开,对任意时间步\(1 \leq t \leq T\),可以得到目标函数有关隐藏状态梯度的通项公式
\[ \frac{\partial L}{\partial \boldsymbol{h}_t} = \sum_{i=t}^T {\left(\boldsymbol{W}_{hh}^\top\right)}^{T-i} \boldsymbol{W}_{qh}^\top \frac{\partial L}{\partial \boldsymbol{o}_{T+t-i}}. \]
由上式中的指数项可见,当时间步数 \(T\) 较大或者时间步 \(t\) 较小时,目标函数有关隐藏状态的梯度较容易出现衰减和爆炸。这也会影响其他包含\(\partial L / \partial \boldsymbol{h}_t\)项的梯度,例如隐藏层中模型参数的梯度\(\partial L / \partial \boldsymbol{W}_{hx} \in \mathbb{R}^{h \times d}\)和\(\partial L / \partial \boldsymbol{W}_{hh} \in \mathbb{R}^{h \times h}\)。 在图中,\(L\)通过\(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_T\)依赖这些模型参数。 依据链式法则,有
\[ \begin{aligned} \frac{\partial L}{\partial \boldsymbol{W}_{hx}} &= \sum_{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \boldsymbol{h}_t}, \frac{\partial \boldsymbol{h}_t}{\partial \boldsymbol{W}_{hx}}\right) = \sum_{t=1}^T \frac{\partial L}{\partial \boldsymbol{h}_t} \boldsymbol{x}_t^\top,\\ \frac{\partial L}{\partial \boldsymbol{W}_{hh}} &= \sum_{t=1}^T \text{prod}\left(\frac{\partial L}{\partial \boldsymbol{h}_t}, \frac{\partial \boldsymbol{h}_t}{\partial \boldsymbol{W}_{hh}}\right) = \sum_{t=1}^T \frac{\partial L}{\partial \boldsymbol{h}_t} \boldsymbol{h}_{t-1}^\top. \end{aligned} \]